É recomendado a leitura dos principais conceitos básicos de teoria dos grafos disponível no link:
Introdução a conceitos básicos
Para realizar esse tutorial é necessário ter instalado os seguintes softwares:
- WinPython (WINDOWS)
- Anaconda (WINDOWS/LINUX/MAC OS)
Em ambos, o sofware Spyder estará incluso na instalação.
Caminhadas aleatórias
Dado um grafo G, uma caminhada aleatória é um dos modos em que se pode percorrer um grafo, ou seja, partindo de um vértice qualquer, escolhe-se um vértice adjacente para ir em seguida. É necessário saber quantas vezes um vértice v foi visitado para que possamos ter uma noção de quais vértices foram mais visitados que os outros. Podemos implementar isso com um vetor, onde cada posição representa um vértice do grafo e o conteúdo em cada posição representa o número de vezes que o vértice foi visitado. Esse vetor é chamado de esquema de distribuição estacionária;
Podemos estabelecer 3 formas de calcular a distribuição estacionária:
- Teórica
A distribuição estacionária teórica é dada pela fórmula w(i)= d(vi) / 2*|E|, onde w(i) é a distribuição estacionária relativa á vi, d(vi) é o grau do vértice vi e |E| é a quantidade total de arestas do grafo.
W = [ d(v1)/2*|E| , d(v2)/2*|E| , d(v3)/2*|E| , … , d(vn)/2*|E| ]
O código em python é dado abaixo:
Fazemos uma referência a biblioteca networkx como nx.
O gráfico escolhido para analisar é o grafo football.gml disponível em [ Grafo Football ]
Para a leitura do grafo é necessário que ele esteja salvo na mesma pasta do projeto criado.
G= nx.read_gml("nome do grafo")
Lê o grafo e atribui a variável G
Criamos uma classe chamada caminhadas aleatórias. Vamos definir todas as formas de calcular a distribuição estacionária como métodos dessa classe:
Em seguida, definimos o método distribuicaoEstacionariaTeorica que recebe como parâmetro um grafo G.
A variável w é um vetor que armazenará a distribuição estacionária de cada nó.
D recebe um dicionário dos graus dos vértices do grafo G através da função nx.degree(G).
N recebe o número de nós disponível no grafo G através da função G.number_of_nodes()
E recebe o número de arestas através da função G.number_of_edges().
Logo após percorremos todos os vértices armazenando a distribuição estacionária de cada um em w
O resultado obtido para o grafo football.gml é o seguinte:
*Observação: A leitura da distribuição estacionária de cada vértice é feita por linhas.
- Power Method
O Power Method é uma maneira de calcular a distribuição estacionária de um vértice através da sua matriz de adjacência (explicada no post de introdução a teoria dos grafos).
Então, dado um W0 qualquer onde a soma dos valores do vetor seja 1, por exemplo W0[1/n,1/n,...,1/n], onde n é igual ao número de vértices do grafo e |W0| = |V|, devemos multiplicar W0 por uma matriz Pk (matriz de probabilidade de visita de um vértice) onde k é um número inteiro e P é definido como:
P=D-1*A,
onde D é uma matriz que tem 1/d(vi) para os elementos da diagonal principal e 0 para os demais
A é a matriz de adjacência do grafo G.
Primeiramente, vamos aplicar o power method com k=5, depois com k=100.
Veremos que quanto maior o K aplicado, mais próximo da distribuição estacionária teórica o resultado estará.
Definimos o método powerMethod (l.31) que recebe como parâmetro um grafo G e um inteiro k.
A seguir (l.32,33,34) declaramos as principais variáveis utilizadas:
W0 = armazenará um vetor com a função escolhida em cada índice (nesse caso, escolhemos W0 como sendo [1/|v|,1/|v|...1/|v|] onde |v| o número de vértices do grafo G.(linha.32)
V= armazena o número de vértices que o grafo G tem através da função G.number_of_nodes() (linha 33)
D= armazena um dicionário contendo o grau de cada vértice de G através da função nx.degree(G) (linha 34)
Na linha 37, definimos Delta, utilizando uma função da bibioteca numpy(np), np.zeros() que define uma matriz preenchida por zeros do tamanho VxV (lembrando que V é o número de vértices de G)
Na linha 39,40 colocamos em cada índice do vetor W0, 1/V.
Na linha 42, a variável A é definida como a matriz de adjacência de G utilizando a função contida na biblioteca networkx (adjacency_matrix()).
Na linha 44, j controlará quando a linha e coluna da matriz Delta forem iguais, ou seja, só vamos alterar a diagonal principal da matriz Delta como explicado acima.
A diagonal principal da matriz Delta será dada pela função 1/d(vi), ou seja, 1/grau do vértice i. Já temos um dicionário D que armazena em cada índice i o grau do vértice i.
A matriz P será A*Delta (linha 49)
O loop definido nas linhas 51 e 52 eleva P à k.
Obs: a função dot faz a multiplicação de duas matrizes e faz parte da biblioteca numpy
Por fim, multiplicamos P e W0 para determinarmos a função estácionária de cada vértice utilizando o power method.
Os resultados foram os seguintes:
Para k=5
Para k=100
Conclusão:
Podemos observar que quanto maior o k fornecido, mais próximo da distribuição estacionária teórica o power method chegará.
Distribuição Estacionária pelo "Andar do bêbado" (Caminhada Aleatória)
De fato, a forma de calcular essa distribuição estacionária é a caminhada aleatória, pois seus dados são gerados aleatoriamente, diferente das outros métodos mostrados acima.
A ideia geral é partindo de um vértice inicial a caminhada é feita escolhendo um vértice aleatório para prosseguir. Para que possamos ter uma noção da probabilidade de um vértice x ter sido escolhido durante a caminhada podemos definir uma variável de contagem de quantas vezes o vértice x foi escolhido dividido pelo tamanho da caminhada, isto é, a quantidade de nós visitados.
P(vi) = vezes que v foi visitado / quantidade de vértices
visitados
Para que a escolha do vértice seja aleatório, iremos utilizar a função random()
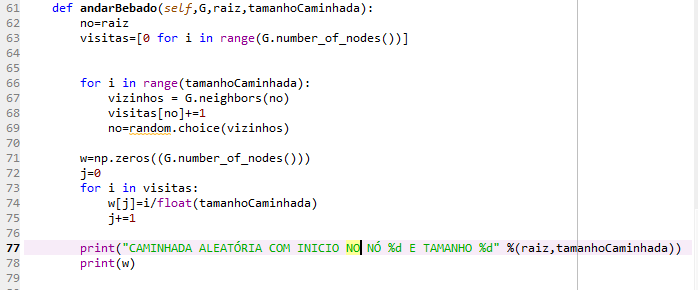
O método andarBebado recebe como parâmetro um grafo G, uma raiz que é o no que começaremos caminhada e um tamanho de caminhada, que é quantos nós iremos visitar.
A variável nó recebe a raiz fornecida para que não perdemos a referência
O vetor visitas é inicialmente iniciado com 0 (linha 63)
A linha 66 define um loop que elaborará uma caminhada de tamanhoCaminhada fazendo:
1. Pegando todos os vizinhos do nó atual (linha 67)
2. Incrementando as visitas do nó atual (linha 68)
3. Escolhendo um nó aleatório para prosseguir (linha 69)
Logo, definiremos um vetor w que de fato armazenará a definição estacionaria de cada vértice.
Na linha 74 é feito um loop que percorrerá o vetor pegando o valor de visitas para cada vértice, dividindo pelo tamanho da caminhada e armazenando em w.
Foram realizadas as seguintes consultas:
1. Dois nós distintos com tamanho de caminhada = 100
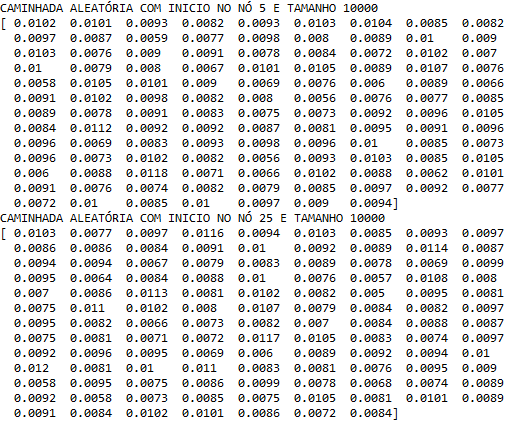
2. Dois nós distintos com tamanho de caminhada = 10000
Conclusão:
Na caminhada aleatória com tamanho da caminhada = 100 podemos observar que as duas execuções com os vértices 5 e 25 produzem resultados diferentes em vários pontos. Isso acontece porque a caminhada tem o valor muito pequeno, o que faz com que os vértices mais distantes não cheguem a ser alcançados.
Na caminhada aleatória com tamanho da caminhada=10000 podemos perceber que os valores se aproximam mais da distribuição estacionária teórica. Como conclusão, quanto maior o tamanho da caminhada, mais próximo a distribuição estacionária probabilística estará da distribuição estacionária teórica.
